在互联网算法领域持续深耕，带领团队解决各种复杂模型与架构问题的过程中，我逐渐意识到一个重要的观点：算法岗位的竞争，远不止于“刷题熟练”或“调参技巧”这些表层能力。当工作深入到最前沿的难题和核心技术时，真正决定成败的关键，并非对各类模型框架的机械记忆，也不是对参数组合的盲目尝试，而是扎实的数学基础，以及由此产生的抽象思维和逻辑构建能力。

很多人对算法岗存在误解，认为只要掌握机器学习的基础理论、了解主流模型的应用场景，就能顺利进入该领域。虽然这些是入门的基本条件，但在面对大规模高维数据的特征提取、非结构化数据的建模优化、复杂系统的稳定性验证等关键问题时，仅靠浅层次的知识储备往往难以应对。

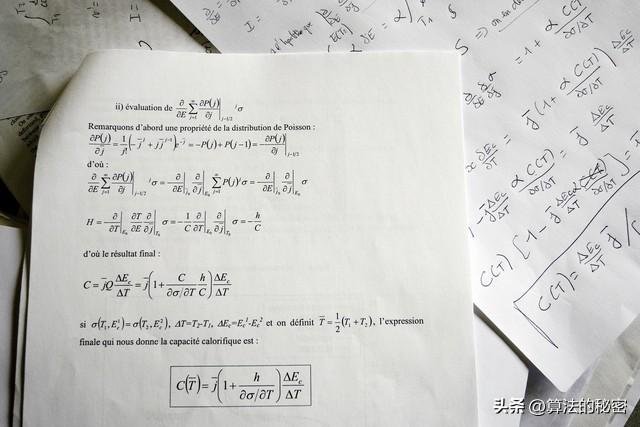
此时，支撑我们突破瓶颈的，往往是泛函分析中算子的性质与空间的映射关系——当我们思考如何构建更稳定的特征空间时，本质上是在寻找合适的算子，实现从原始数据空间到特征空间的有效转换；是微分几何中流形上的测地线与曲率计算——在处理高维数据降维与聚类时，流形学习的核心在于挖掘数据在低维流形上的内在结构，测地线的存在为数据点之间的“真实距离”提供了数学依据；也是抽象代数中群、环、域的结构与不变量——在设计模型损失函数时，不变量的特性能确保模型在特定变换下的稳定性，提升算法的泛化能力。

这些扎根于高等数学、线性代数、概率论与统计学，延伸至泛函分析、微分几何、抽象代数等领域的知识，并非只是理论上的空谈，而是解决实际问题的重要基础。当我们调试深度学习模型的收敛性时，背后涉及的是最优化理论中的梯度下降收敛条件与凸性分析；当我们构建推荐系统中的协同过滤模型时，矩阵分解的秩亏问题与正则化策略，离不开线性代数的矩阵理论；当我们尝试用强化学习解决复杂的序列决策问题时，马尔可夫决策过程的数学建模是整个算法设计的核心。

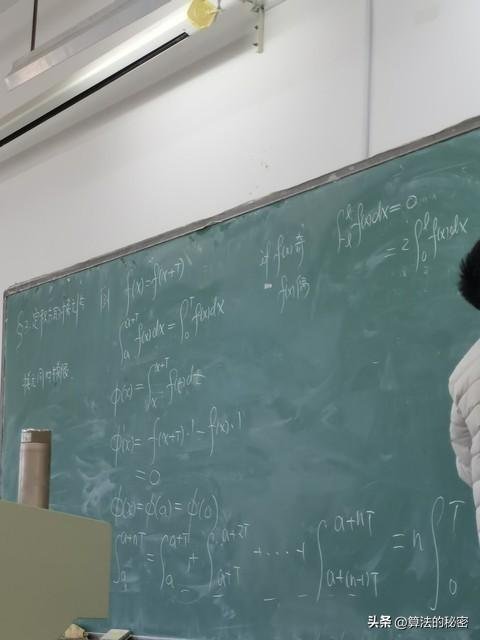
而比具体数学知识更重要的是，在长期数学训练中培养出的抽象思维和逻辑构建能力。算法的本质，是将现实世界中的复杂问题转化为数学模型，再通过逻辑推理找到解决方案。这种抽象能力，使我们能够穿透问题表面，抓住核心矛盾；这种逻辑构建能力，使我们能在零散的知识点中建立严谨的理论体系，确保算法的正确性和可解释性。

对于从事算法核心工作的人员来说，数学从来不是可有可无的加分项，而是立足行业的根本。那些在深夜反复思考的，不是具体的代码，而是泛函空间中的算子、流形上的测地线、代数结构中的不变量。它们是算法的灵魂，也是我们在技术前沿不断突破的关键力量。